标签：
norm表示正态分布：
rnorm(x):表示生成随机x个正态分布的序列，random
dnorm(x):输出正态分布的概率密度函数，density function————plot(dnorm(x)),画出密度曲线
pnorm(x):输出正态分布的分布函数，概率函数，probability function
【对于连续分布，分布函数就是从负无穷到x对概率密度函数的积分的结果】
qnorm(p):分位函数，quantile fuction。给出一个概率p,函数返回一个x，表明概率为p时的x值。
[设连续随机变量X的分布函数为F(X)，密度函数为p(x)。那么，对任意0<p<1的p，称F(X)=p的x为此分布的分位数，或者下侧分位数。简单的说，分位数指的就是连续分布函数中的一个点，这个点对应概率p。]
help(dnorm):
dnorm gives the density, pnorm gives the distribution function, qnorm gives the quantile function[分位函数], and rnorm generates random deviates.
dnorm(x, mean = 0, sd = 1, log = FALSE) 默认情况下是标准正态分布
pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
rnorm(n, mean = 0, sd = 1)
x, q: vector of quantiles. 向量的分位数
p:vector of probabilities. 向量概率
n:number of observations. If length(n) > 1, the length is taken to be the number required.
mean:vector of means.
sd:vector of standard deviations.
log, log.p:logical; if TRUE, probabilities p are given as log(p).
如果log.p=TRUE，则在用qnorm(p)计算时变成qnrom(log(p))来计算。【由于概率p介0~1之间，当超出这个范围后，用此方法相当于是扩大的计算范围。如qnorm(-.5,log.p=F) == qnorm(log(-.5),log.p=F)，后来验证，这种理解是错误的，正确的是什么？】
lower.tail:logical; if TRUE (default), probabilities are P[X ≤ x] otherwise, P[X > x].
如果lower.tail=TRUE，则计算的是左侧面积的概率，即P[X ≤ x]；否则就是右侧 P[X > x]=1-P[X ≤ x]
正态分布函数：
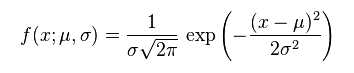，此式中当 μ=0, σ=1时，
标准正态分布函数为：
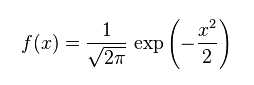
便于理解公式的几个有趣例子：
dnorm(0) == 1/sqrt(2*pi)，此时x=0, μ=0, σ=1
dnorm(1) == exp(-1/2)/sqrt(2*pi),下面式子的等价写法
dnorm(1) == 1/sqrt(2*pi*exp(1)),此时x=1, μ=0, σ=1
对于分位数的补充：
分位数函数：分位数函数是累积分布函数【概率函数】的反函数，也就是说，给定概率值，计算出随机变量的取值（左侧分位数）。
常用的有四个分布的分位数：
标准正态分布，qnorm(p, mean=0, sd=1)
Student’s (t) , qt(p,df=N,ncp=0)
卡方分布：qchisq(p, df=N,ncp=0)
Fisher-Snedecor：qf(p, df1,df2,ncp=0)
特例：
四分位数：四分位数是统计学中分位数的一种，即把所有的数值从小到大朴烈并分为四等分，处于三个分割点的数就是四分位数。
标签：
原文地址：http://www.cnblogs.com/ysdx2013/p/4738711.html
