标签：
给定一个离散变量，我们观察它的每一个取值所包含的信息量的大小，因此，我们用
来表示信息量的大小，概率分布为
。当p(x)=1时，说明这个事件一定会发生，因此，它带给我的信息为0.（因为一定会发生，毫无悬念）
如果x和y独立无关，那么：
他们之间的关系为：
（p(x)=1时，h(x)=0，负号为了确保h(x)为正，这里取2为底是随机的，可以取其他的正数（除了1））
因此，对于所有x的取值，它的熵有：
注：
，当遇到
时，
这里插一段信息熵的解释：
———————————————————————————————信息熵—————————————————————————————————————————————————
信息熵是对信息的度量，那什么又是信息呢？ 直观上的理解就是，知道我们原来不知道的事物就是获得信息的过程，因此对于个人来说，一件事的未知性越大，即不确定性越大，相应的信息就应该越大，传输或者存储应该付出更多的代价。例如我们说太阳从东边升起，这是一件必然的事，听到这句话没有获得任何信息，因此它的熵是0，信息论中信息与不确定性等价。
有了这个直观认识，可以对其数学化，在数学中表达不确定性的就是概率。在上面的例子中，我们讨论信息的时候，实质上是在说一件事发生的概率大小，这件事有一定概率发生。我们说信息熵是大是小，要明确是哪个随机变量的信息熵，这样才不至于迷糊。一件事发生的概率大，那么它的熵就小，一件事发生的概率小，那么它的熵就大。
问32支球队哪个得冠军，我们可以设一个随机变量X表示得冠军的球队，假设每个球队得冠军的概率相等，那么一个球队的熵x1 表示为 h(x1) = logp(x1), 所有球队求和得到X的熵：
一般情况对数取2为底，表示X对应的比特数。
总之，信息熵可以让我们定量的说出信息有多少，让一个抽象的概念可以定量的描述。另外，当我们说到信息熵的时候首先明确一下是哪个随机变量的信息熵，该随机变量的样本空间是什么，然后运用概率论的知识就可以求出来了。需要注意的是信息量的多少和信息的重要性没有必然的联系，信息熵只是在数量上给了一个数值，并非表示该信息的重要性。
———————————————————————————————————————————————————————————————————————————————————
举个例子：
假设你要发送一个离散变量给别人，这个离散变量有8个取值，并且这8个取值取到的概率相同，那么，这个变量的熵为：
另外举个例子：
一个变量含有8个状态值，
，相应的概率为：
，那么，它的熵为：
从上面的例子可以看出，不均匀分布的信息熵小于均匀分布的信息熵。这是为什么呢？
因为，如果我们想要吧这个变量发送给别人，一种方法就是用3位来表示每一个数，那么它的平均译码长度为3.
这里还有一种别的方法就是：
用
来表示。
平均的译码长度为2即可：
为了消除二异性，没有比这个更短的了。
（再次感受到了数学之美）
我们可以从另一个角度去理解信息熵：
假设有N个相同的物品，第i个箱子中有
个物品。对于第i个箱子，首先它有N种选择去取第一件物品，N-1种选择去取第二件物品，因此，对于一个箱子而言，它有N!种选择。但是，对于同一个箱子中的物品，我们并不希望加以区分，因此，对于第i个箱子而言，它有
种排序方式，因此，总的组合方法数multiplicity 为：
其中，熵为其取对数：
当
时，
，
因此，
。
对于一个特定的状态，即一个实例，称作一个“微观状态”；
对于所有的状态而言，即称作一个“宏观状态”，而w就是一个宏观状态。
对于一个特定的状态xi而言，它的概率为：
当每个微观状态发生的概率集中出现在少数值附近，往往它的熵会较小。
如图所示：
假设有M个状态，我们试图去最大化熵：
我们发现，当
相等时，相应的熵为：
，这个状态下，熵达到了最大值。
现在，我们假设x为连续型变量，我们求偏导：
其中，Iij为单位矩阵。
根据中值定理，我们可以得出：
假设变量x落在第i个箱子中的概率为：
其中：
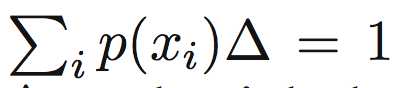
而当
趋近于0时，上式最右侧第二项趋近于0，而第一个项则趋近的表达式称为微分熵(differential entropy)：
对于连续变量而言，熵如何取最大？
首先，它满足如下约束：
使用拉格朗日乘子法可以得到：
简化得到：
可以发现，微分熵最大的概率分布为高斯分布。
我们在计算时，并没有假定微分熵一定是非负的，因此，它并不是一个必要条件。
正态分布的微分熵表达式：
可以发现，随着方差的增大，熵变大。
相对熵（relative entropy）又称为KL散度（Kullback–Leibler divergence，簡稱KLD），信息散度（information divergence），信息增益（information gain）。
这并非是对称的，即
，仅仅在p(x)=q(x)的时候成立
—————————————————————————————————————————————————————————————————————————
—————————————————————————————————————————————————————————————————————————
凸函数：
性质：
其中，
且
琴生不等式（Jensen‘s inequality）
琴生不等式（Jensen‘s inequality）以丹麦数学家约翰·琴生（Johan Jensen）命名。它给出积分的凸函数值和凸函数的积分值间的关系。琴生不等式有以下推论：过一个凸函数上任意两点所作割线一定在这两点间的函数图象的上方，即：
概率论的版本
以概率论的名词，
是个概率测度。函数
换作实值随机变数
（就纯数学而言，两者没有分别）。在
空间上，任何函数相对于概率测度
是任一凸函数，则
。
E表示期望。连续型变量的jensen不等式为：
把jensen不等式应用在相对熵上面，得到：
假设未知真实分布为
，我们希望使用一个参数模型
结合N个观测数据来确定一个最优的
来模拟真实分布。一种自然的方法是使用KL距离做为误差函数，以最小化
将上面的误差函数相对于参数
互信息描述了两个变量之间互相包含关于对方的信息量。定义为两个分布
和
之间的KL距离
根据相对熵的非负性可知，互信息是非负的，当仅且当两个变量相互独立时互信息为零。
由此可知，互信息可以看作，当已知一个变量的情况下，另一个变量不确定性降低的程度。
【PRML读书笔记-Chapter1-Introduction】1.6 Information Theory
标签：
原文地址：http://www.cnblogs.com/XBWer/p/4738813.html
