标签:
问题:给出一系列的坐标点,请找出哪些点可以围成一个面积最大的凸多边形?
思路:(1)先寻找最左边的坐标点,这样剩下的点与这个点都可以连成一条直线,寻找斜率最大的点(x0,y0),这个点就是需要找的。
(2)以这个点(x0,y0)为基础,按照上述方法寻找下一个点,以此类推,直到形成一个密闭的多边形。
(3)在寻找点的过程中要保证这个过程是顺时针方向进行。
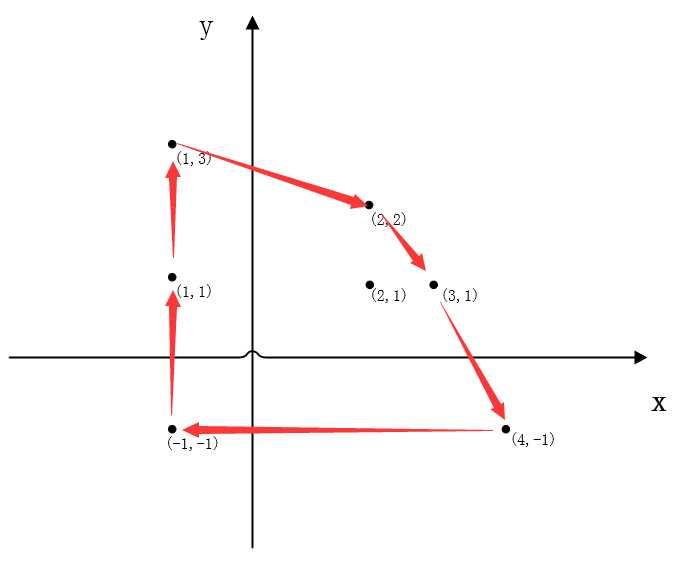
方法:我们将以一组坐标值为例来讲解算法的实现。如下图所示,从坐标(-1,-1),(1,1),(1,3),(2,2),(2,1),(3,1),(4,-1)中找到可以围成最大凸多边形的坐标组。
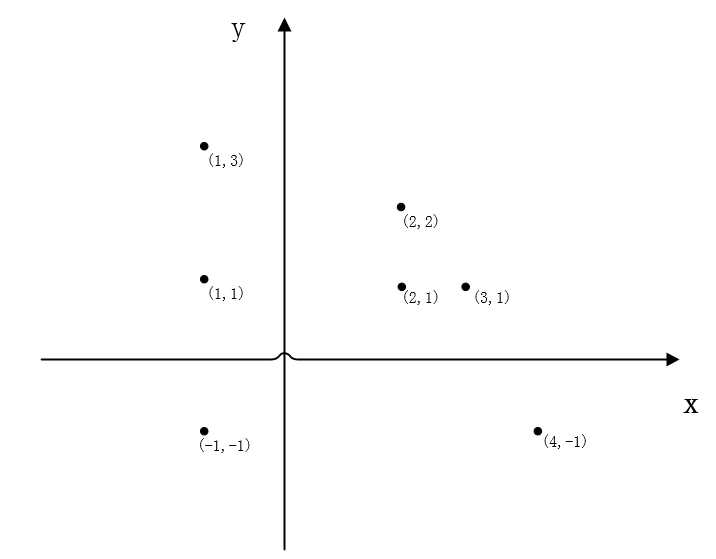
(1)首先我们应该考虑到在用斜率来确定下一个坐标时,斜率值为无穷的情况(也就是要找的下一个坐标点的x值与原坐标点一样)。其实通过上图我们可以发现,在寻找下一个坐标点的时候,只有在最左边和最右边才会出斜率为无穷的情况。因为位于中间的坐标点总是以顺时针方向寻找下一个点,不可能出现原坐标点和下一个坐标点的x值相同的情况。而位于两边的坐标则会出现这种情况,但是这种情况也比较特殊,因为出现在最左边和最右边上的坐标点全部都应该是最大凸多边形上的点。因此我们可以先确定最左和最右为凸多边形上的点,剩下的点则以”思路“中提供的方法来寻找。
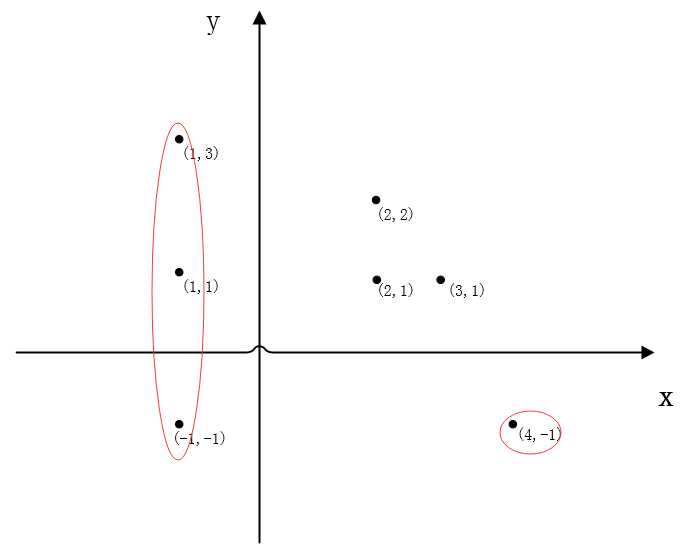
(3)接下来将顺时针寻找坐标点的过程,分为从左到右寻找上边界的过程和从右到左寻找下边界的过程。从左到右过程的起始坐标应该为最左边的坐标中(若存在多个)纵坐标最大的那个(也就是图示中的(1,3)),结束坐标应该为最右边的坐标中纵坐标最大的那个。而从右到左过程的起始坐标点则分别是最右边和最左边最小的两个坐标。
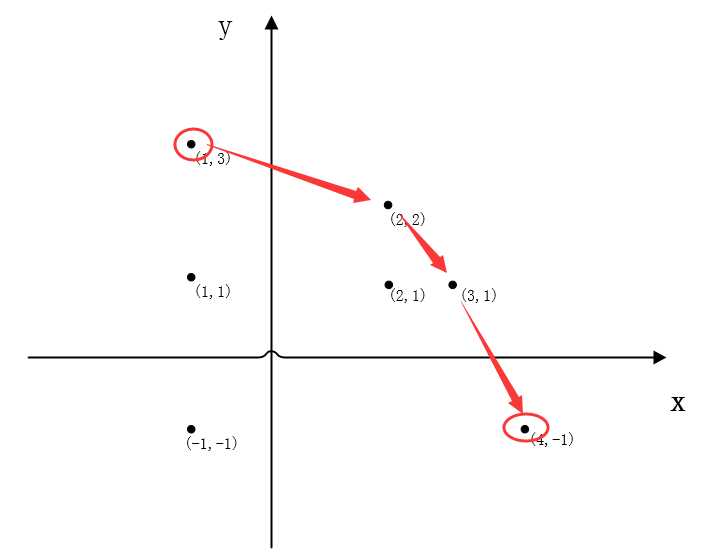
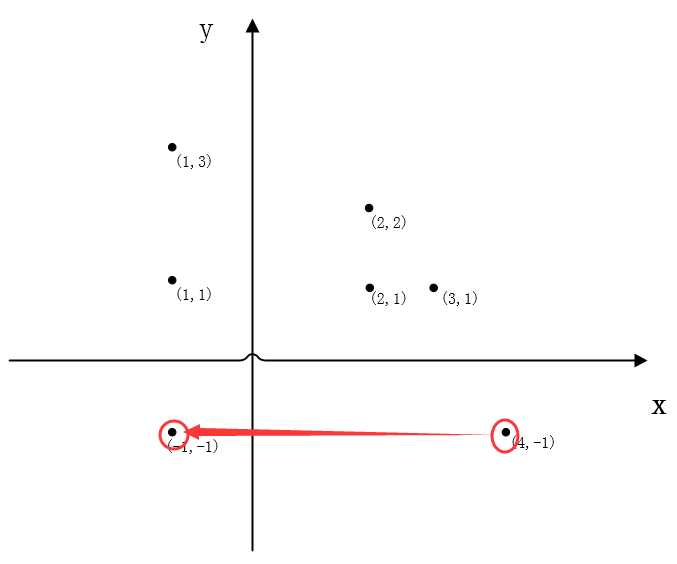
(3)最后求得的中间坐标和最左和最右坐标就是组成最大凸多边形的所有坐标点。
Java代码实现:
输入:7;-1,-1;1,1;1,3;2,2;2,1;3,1;4,-1
输出:6;-1,-1;1,1;1,3;2,2;3,1;4,-1

import java.awt.Point; import java.util.ArrayList; import java.util.HashMap; import java.util.Map; import java.util.Scanner; import java.util.StringTokenizer; public class Main { public static Map<Integer, ArrayList<Point>> readData(){ Scanner s = new Scanner(System.in); String input = null; Map<Integer, ArrayList<Point>> pts = new HashMap<Integer, ArrayList<Point>>(); if(s.hasNext()){ input = s.nextLine(); } StringTokenizer st = new StringTokenizer(input, ",;"); st.nextToken(); while(st.hasMoreTokens()){ Integer x = Integer.parseInt(st.nextToken()); Integer y = Integer.parseInt(st.nextToken()); ArrayList<Point> v = pts.get(x) == null ? new ArrayList<Point>() : pts.get(x); v.add(new Point(x, y)); pts.put(x, v); } int key = 0; Map<Integer, ArrayList<Point>> indexPts = new HashMap<Integer, ArrayList<Point>>(); for(java.util.Map.Entry entry : pts.entrySet()){ indexPts.put(key, (ArrayList<Point>)entry.getValue()); key++; } return indexPts; } @SuppressWarnings({ "rawtypes", "unchecked" }) public static void main(String[] args) { ArrayList<Point> ptOkList = new ArrayList<Point>(); Map<Integer, ArrayList<Point>> pts = readData();//读取数据并存储到map中 int i = 0; Point startUp = pts.get(0).get(0); Point startBottom = pts.get(0).get(0); Point endUp = pts.get(pts.size() - 1).get(0); Point endBottom = pts.get(pts.size() - 1).get(0); for(i = 0; i < pts.get(0).size(); i++){ if(pts.get(0).get(i).y > startUp.y){ startUp = pts.get(0).get(i); } if(pts.get(0).get(i).y < startBottom.y){ startBottom = pts.get(0).get(i); } } for(i = 0; i < pts.get(pts.size() - 1).size(); i++){ if(pts.get(pts.size() - 1).get(i).y > startUp.y){ endUp = pts.get(pts.size() - 1).get(i); } if(pts.get(pts.size() - 1).get(i).y < startBottom.y){ endBottom = pts.get(pts.size() - 1).get(i); } } Point startPt = startUp; int index = 0; Point p = startUp; while(true){ float k = -Float.MAX_VALUE; for(i = index + 1; i < pts.size(); i++){ //int index_ = index; for(int j = 0; j < pts.get(i).size(); j++){ Point temp = pts.get(i).get(j); float kk = (temp.y - startPt.y) / (temp.x - startPt.x); if(kk > k){ p = temp; k = kk; index = i; } } } startPt = p; if(startPt == endUp){ break; } ptOkList.add(startPt); } startPt = endBottom; index = pts.size() - 1; p = endBottom; while(true){ float k = -Float.MAX_VALUE; for(i = index - 1; i >= 0; i--){ //int index_ = index; for(int j = 0; j < pts.get(i).size(); j++){ Point temp = pts.get(i).get(j); float kk = (temp.y - startPt.y) / (temp.x - startPt.x); if(kk > k){ p = temp; k = kk; index = i; } } } startPt = p; if(startPt == startBottom){ break; } ptOkList.add(startPt); } for(i = 0; i < pts.get(0).size(); i++){ ptOkList.add(pts.get(0).get(i)); } for(i = 0; i < pts.get(pts.size() - 1).size(); i++){ ptOkList.add(pts.get(pts.size() - 1).get(i)); } System.out.print(ptOkList.size()); for(i = 0; i < ptOkList.size(); i++){ System.out.print(";" + ptOkList.get(i).x + "," + ptOkList.get(i).y); } } }
标签:
原文地址:http://www.cnblogs.com/liujinyao/p/4738599.html