标签:
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 12822 | Accepted: 3347 |
Description
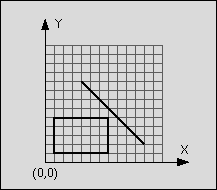
Input
Output
Sample Input
1 4 9 11 2 1 5 7 1
Sample Output
F
解题思路:
题意很清楚,就是判断一个线段是否和矩形相交。而所谓“相交”,但是这个相交的定义是线段在矩形内或者线段与矩形的边相交。
判断方法:
判断线段的两端点是否在矩形内,若是,则线段在矩形内。
判断线段是否与矩形相交,即是否和矩形的四条边中的任意一条边相交(规范相交和不规范相交都算)。
其实这是一个很好的模板题,注意处理下就可以了!
ACcode:
#include<iostream> #include<stdio.h> #include<string> #include<map> #include<set> #include<queue> #include<stack> #include<string.h> #include<stdlib.h> #include<math.h> #include<algorithm> #define PI 3.1415926 #define MOD 10000000007 #define N 1000005 #define INF 0x7fffffff using namespace std; typedef long long LL; const double eps=1e-8; //点 struct point { double x,y; }; //线段 struct line { point p1,p2; } l; //面 struct poly { int n;//几个面 double area; point plist[15]; } rec; //点乘 double dotdel(double x1,double y1,double x2,double y2) { return x1*x2+y1*y2; } //叉乘 double crossmul(double x1,double y1,double x2,double y2) { return x1*y2-x2*y1; } //判断是否为0,达到一定精度即认为成立 int cmpzero(double d) { return (fabs(d)<eps)?0:(d>0?1:-1); } //右手螺旋定则,1:a在cd右侧,-1:a在cd左侧,0:三点共线 int cross(point a,point c,point d) { return cmpzero(crossmul(a.x-c.x,a.y-c.y,d.x-c.x,d.y-c.y)); } //在cross(a,c,d)==0的基础上,可判断点a是否在cd内部 int between(point a,point c,point d) { return cmpzero(dotdel(c.x-a.x,c.y-a.y,d.x-a.x,d.y-a.y))!=1; } //两线段相交情况:0:不相交,1:规范相交,2:不规范相交(交于端点或重合) int seg_intersect(point a,point b,point c,point d) { int a_cd=cross(a,c,d); if(a_cd==0 && between(a,c,d)) return 2; int b_cd=cross(b,c,d); if(a_cd==0 && between(a,c,d)) return 2; int c_ab = cross(c, a, b); if (c_ab == 0 && between(c, a, b)) return 2; int d_ab=cross(d,a,b); if(d_ab==0 && between(d,a,b)) return 2; if((a_cd^b_cd)==-2 && (c_ab^d_ab)==-2) return 1; return 0; } //使用有向面积法判断点是否在多边形内 bool point_in_poly(point p) { double s=0.0; for(int i=0; i<rec.n; i++) s+=fabs(crossmul(rec.plist[i].x-p.x,rec.plist[i].y-p.y,rec.plist[(i+1)%rec.n].x-p.x, rec.plist[(i+1)%rec.n].y-p.y)); if(cmpzero(s-rec.area)==0) return true; else return false; } //判断线段是否与多边形相交 bool rec_seg_intersect() { if(point_in_poly(l.p1) && point_in_poly(l.p2)) return 1; else if(seg_intersect(l.p1,l.p2,rec.plist[0],rec.plist[1]) || seg_intersect(l.p1,l.p2,rec.plist[1],rec.plist[2]) || seg_intersect(l.p1,l.p2,rec.plist[2],rec.plist[3]) || seg_intersect(l.p1,l.p2,rec.plist[3],rec.plist[0])) return 1; return 0; } //计算多边形面积 void getarea() { double s=rec.plist[0].y*(rec.plist[rec.n-1].x-rec.plist[1].x); for(int i=1; i<rec.n; i++) s+=rec.plist[i].y*(rec.plist[i-1].x-rec.plist[(i+1)%rec.n].x); rec.area=s; } int main() { int T; double x1,y1,x2,y2,t; scanf("%d",&T); while(T--) { scanf("%lf%lf%lf%lf",&l.p1.x,&l.p1.y,&l.p2.x,&l.p2.y); scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); if(x1>x2) { t=x1; x1=x2; x2=t; } if(y2>y1) { t=y1; y1=y2; y2=t; } rec.n=4; rec.plist[0].x=x1; rec.plist[0].y=y1; rec.plist[1].x=x1; rec.plist[1].y=y2; rec.plist[2].x=x2; rec.plist[2].y=y2; rec.plist[3].x=x2; rec.plist[3].y=y1; getarea(); puts(rec_seg_intersect()?"T":"F"); } return 0; }
标签:
原文地址:http://www.cnblogs.com/gaojupeng/p/4739506.html