标签:
给定a和n,计算a+aa+aaa+aaaa+...+a...a(n个a) 的和。 输入描述: 测试数据有多组,以文件结尾。每行输入a,n(1<=a,n<=1000000)。 输出描述: 由于结果可能比较大,所以请输出答案mod 1000000007。
仔细审题,假设a=2,n=6;那么要求的和Σ = 2 + 22 + 222 + 2222 + 22222 + 222222
貌似也不难,只要知道n的长度,只需要把这些数值加起来不就行了吗?
再看题中提示:由于结果可能比较大,所以请输出答案mod 1000000007。
如果n很大时,超过定义数据类型的最大长度,这道题使用传统意义上的加法运算,貌似有点不可取。
看一下这个数据(a=3,n=8)
3
33
333
3333
33333
333333
3333333
33333333
个位数的和是 8 * 3 = 24,十位数的和是7 * 3 + 2= 21 + 2 = 23 (2来自个位和24的进位2),百位数的和是6 * 3 + 2 = 18+2=20 (2来自十位和23的进位2)......通过这个逻辑,我们可以推算出计算 给定a和n,计算a+aa+aaa+aaaa+...+a...a(n个a) 的和 的算法
1 #include<stdio.h> 2 #define MAX 1000000 3 int main() 4 { 5 int a = 3,n= 99; 6 int i,tmp=0; 7 char array[MAX+1]= {0}; 8 //倒序相加 9 for(i=0; i<n; i++) 10 { 11 tmp = a*(n-i)+tmp; 12 array[i] = tmp%10; 13 tmp = tmp/10; 14 } 15 while(tmp>0) 16 { 17 array[n++] = tmp%10; 18 tmp = tmp/10; 19 } 20 //倒序输出 21 for(i=n-1; i>=0; i--) printf("%d",array[i]); 22 printf("\n"); 23 24 return 0; 25 }
运行结果:

可见结果的确很长,题中输出描述:
由于结果可能比较大,所以请输出答案mod 1000000007
现在要做的事情就是如何将上面那么长的数据结果mod 1000000007。
我使用下面这种思路,比如有一个数 123456789,计算 123456789 mod 100007的值
第一步:123456789 - 100007000 = 23449789
第二步:23449789 - 10000700 = 13449089
第三步:13449089 - 10000700 = 3448389
第四步:3448389 - 1000070 = 2448319
第五步:2448319 - 1000070 = 1448249
第六步:1448249 - 1000070 = 448179
第七步:448179 - 100007 = 348172
第八步:348172 - 100007 = 248165
第九步:248165 - 100007 = 148158
第十步:148158 - 100007 = 48151
最终求得 123456789 mod 100007 = 48151
仔细想为什么呢?
既然思路已经有了,那么就上代码了。
1 #include<stdio.h> 2 #define MAX 1000000 3 int main() 4 { 5 int a = 3,n= 99; 6 int i,tmp=0; 7 char array[MAX+1]= {0}; 8 //倒序相加 9 for(i=0; i<n; i++) 10 { 11 tmp = a*(n-i)+tmp; 12 array[i] = tmp%10; 13 tmp = tmp/10; 14 } 15 while(tmp>0) 16 { 17 array[n++] = tmp%10; 18 tmp = tmp/10; 19 } 20 //倒序输出 21 for(i=n-1; i>=0; i--) printf("%d",array[i]); 22 printf("\n"); 23 24 int n1=n; 25 while(n-n1>0 || n1-10>=0) 26 { 27 int b=0; 28 //判断前十位是不是大于1000000007,如果不大于,判断前11位 29 if(!b&&array[n1-1]>1)b=1; 30 if(!b&&array[n1-2]>0)b=1; 31 if(!b&&array[n1-3]>0)b=1; 32 if(!b&&array[n1-4]>0)b=1; 33 if(!b&&array[n1-5]>0)b=1; 34 if(!b&&array[n1-6]>0)b=1; 35 if(!b&&array[n1-7]>0)b=1; 36 if(!b&&array[n1-8]>0)b=1; 37 if(!b&&array[n1-9]>0)b=1; 38 if(!b&&array[n1-10]>7)b=1; 39 if (!b) 40 { 41 n1--; 42 continue; 43 } 44 45 b=0;//是否需要借位 46 if (array[n1-10]>=7) 47 { 48 array[n1-10]-=7; 49 b=0; 50 } 51 else 52 { 53 array[n1-10]+=3; 54 b=1; 55 } 56 57 for(i=9; i>=2; i--) 58 { 59 if(b) 60 { 61 if(array[n1-i]>=1) 62 { 63 array[n1-i]-=1; 64 b=0; 65 } 66 else 67 { 68 array[n1-i]=9; 69 b=1; 70 } 71 } 72 } 73 74 if (n-n1>0) 75 { 76 if(b) 77 { 78 array[n1-1]=array[n1]*10+array[n1-1]-2; 79 } 80 else 81 { 82 array[n1-1]=array[n1]*10+array[n1-1]-1; 83 } 84 array[n1]=‘\0‘; 85 } 86 else 87 { 88 if(b) 89 { 90 array[n1-1]=array[n1-1]-2; 91 } 92 else 93 { 94 array[n1-1]=array[n1-1]-1; 95 } 96 } 97 n1=--n; 98 } 99 100 //倒序输出 101 for(i=n-1; i>=0; i--) printf("%d",array[i]); 102 printf("\n"); 103 104 return 0; 105 }
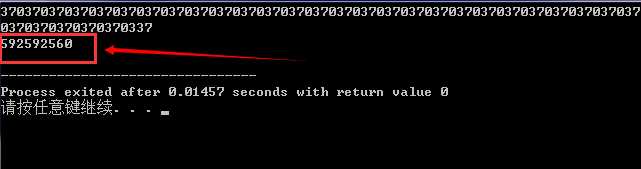
运算结果:
标签:
原文地址:http://www.cnblogs.com/preacher/p/4739585.html