第六周O题（等边三角形个数）

Gerald got a very curious hexagon for his birthday. The boy found out that all the angles of the hexagon are equal to . Then he measured the length of its sides, and found that each of them is equal to an integer number of centimeters. There the properties of the hexagon ended and Gerald decided to draw on it.

He painted a few lines, parallel to the sides of the hexagon. The lines split the hexagon into regular triangles with sides of 1 centimeter. Now Gerald wonders how many triangles he has got. But there were so many of them that Gerald lost the track of his counting. Help the boy count the triangles.

The first and the single line of the input contains 6 space-separated integers a₁, a₂, a₃, a₄, a₅ and a₆ (1 ≤ a_i ≤ 1000) — the lengths of the sides of the hexagons in centimeters in the clockwise order. It is guaranteed that the hexagon with the indicated properties and the exactly such sides exists.

Print a single integer — the number of triangles with the sides of one 1 centimeter, into which the hexagon is split.

This is what Gerald‘s hexagon looks like in the first sample:

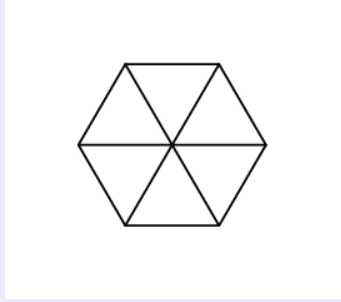
And that‘s what it looks like in the second sample:

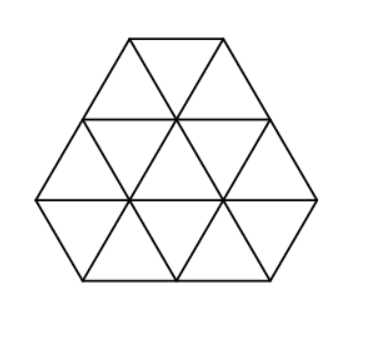
题解;又是一道数学问题，输入六边形的每条边的长度，然后以边长1画等边三角形，统计六边形内部三角形的个数，统计时采用容斥原理即可。

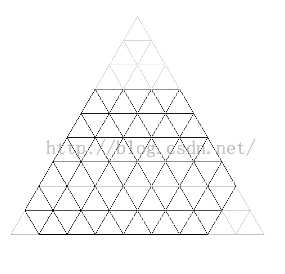
盗图一张。。 

 这里输入的边长为3 4 2 6 1 5   ，通过填补的到一个正三角形，正三角形的边长len就是前三个边a1+a2+a3=9,这个正三角形中含有边长为1的三角形的个数就是len*len=81，然后减去三个角的三角形个数即可，这三个三角形也是正三角形，所以减去的三角形个数就是3*3+2*2+1*1，所以六边形含有的边长为1的三角形个数为81-(3*3+2*2+1*1）=67

 代码：

#include<iostream>
using namespace std;
int main()
{
    int a1,a2,a3,a4,a5,a6;
    cin>>a1>>a2>>a3>>a4>>a5>>a6;
    int len=a1+a2+a3;
    cout<<len*len-a1*a1-a3*a3-a5*a5<<endl;
}