标签:
摘要:
本文主要针对于FCM算法在很大程度上局限于处理球星星团数据的不足,引入了核方法对算法进行优化。
与许多聚类算法一样,FCM选择欧氏距离作为样本点与相应聚类中心之间的非相似性指标,致使算法趋向于发现具有相近尺度和密度的球星簇。因此,FCM很大程度上局限于对球星星团的处理,不具有普遍性。联系到支持向量机中的核函数,可采用核方法将数据映射到高维特征空间进行特征提取从而进行聚类。现阶段,核方法已广泛应用于模糊聚类分析算法。核方法的应用目前已成为计算机智能方面的热点之一,对于核学习的深入研究具有很重要的意义。本文主要讲述将核方法应用到FCM算法中。
一 核方法概述
1. 核方法的简单介绍
核方法起源于支持向量机(SVM)理论,将数据通过特征映射嵌入到相应的特征空间(希尔伯特空间),发现数据在特征空间上的线性模式,进而选取相应的核函数利用输入计算内积,其中特征映射Φ的作用就是将数据重新编码,从而发现数据之间的线性模式。根据对偶解法可得算法所需要的信息位于特征空间上数据点之间的内积,所以可以将内积作为输入特征的直接函数,同时也减少了算法的时间复杂度。因此,核方法常用来处理那些效率低下,特征相似的问题。
核函数是核方法应用的关键,它在很大程度上解决了非线性以及高维数问题。核函数对数据进行隐性的非线性映射,不用具体求出非线性映射,只需计算内积,使算法更为高效和灵活。核函数的本质是解决数据之间的相似问题,核函数可以有很多不同的形式,并且构造方法也多种多样,现已得到了多种核函数,不同的核函数可作为不同的相似度指标,在FCM算法中就是衡量样本点和聚类中心之间的距离。
基于上述分析,我们需要解决非球星星团的聚类分析问题。联系到T.M.Cover的模式可分性定理:一个复杂的模式分析问题映射到高维空间后,会比在低维空间线性可分。结合支持向量机,联系到核方法,可将数据使用Mercer核映射到高维特征空间进行特征提取,选取相应的核函数进行聚类分析。
2. 核方法的研究进展
早在20世纪60 年代就有学者在模式识别中引入了核函数,直到支持向量机成功应用于模式识别,核方法才得到了快速的发展。Scholkopfs等人首先在特征提取中应用到了核学习的思想,提出核主成分分析法(KPCA);之后,Mika、Baudt、Roth等人采用核学习方法将线性判别分析算法拓展为核判别分析算法。核方法的研究逐渐活跃起来,已涌现出了大量算法,经过学者们的不懈努力,核方法现已形成了较完整的学习研究体系。目前针对于核方法的研究大体可以分为:基于核学习的分类算法、基于核学习的聚类算法(核聚类)以及基于核学习的神经网络等研究分支。
核聚类是近年发展起来的一个重要分支,现已取得了丰硕的成果。随着核学习研究的不断深入,核学习已被广泛应用到字符识别、人脸识别、图像检索、目标跟踪、图像处理以及文本归类等各个领域。可以断言,核方法必将有更为广阔的应用前景。
3. 核模糊C均值聚类
该算法选取相应的核函数替代FCM算法中的欧氏距离。结合FCM算法我们来分析一下核模糊C均值聚类,在这里我们可将其表示为KFCM。
我们知道,FCM的目标函数为:
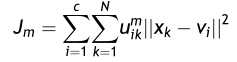
约束条件为:
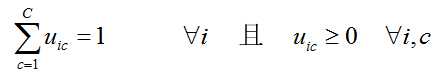
现在要引入核方法,则可将目标函数转化为:
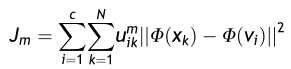
其中Φ指的是特征映射,根据核方法的中的转换技巧,我们可以做如下转换:
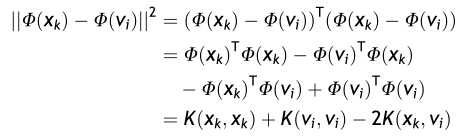
在此选取高斯核:
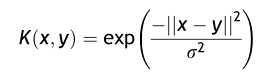 ,根据
,根据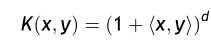 ,
,
结合K(x,x) = 1,则目标函数可转化为:
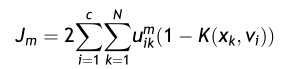
为了最小化目标函数,结合约束条件,求得聚类中心和隶属度矩阵的更新公式分别为:
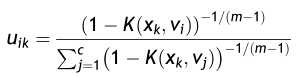
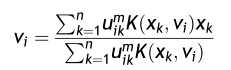
根据上述公式不断迭代求出满足条件的隶属度以及聚类中心从而最小化目标函数,保证算法收敛,具体的算法步骤如下:
算法开始之前必须给定一个由N个L维向量组成的数据集X以及所要分得的类别个数C,自定义隶属度矩阵。
(1)设定类别的个数C和模糊系数m;
(2)初始化隶属度矩阵且满足公归一化条件;
(3)根据公式聚类中心;
(4)根据公式更新隶属度矩阵;
(5)根据矩阵范数比较迭代的隶属度矩阵,若收敛,迭代停止,否则返回(3)。
二 MATLAB实现
在此我们选取同样选取MR图像实现,建立MKFC.m文件,代码如下:
%%%%%MKFCM clear all clc; a=imread(‘MRI.jpg‘); I=imnoise(a,‘salt & pepper‘,0.03); [height,width,c]=size(a); if c~=1 a=rgb2gray(a); end a=double(a); [row,column]=size(a); %% 几个参数 beta = 1000; cluster_num = 4;%将图像分为四类 default_options = [2.0; % exponent for the partition matrix U 300; % max. number of iteration 0.01; % min. amount of improvement 1]; % info display during iteration options = default_options; m = options(1); % p,图像的质量参数 iter_num = options(2); % Max. iteration 最大迭代次数 threshold = options(3); % Min. improvement 最小进化步长 display = options(4); % Display info or not 显示信息与否 costfunction = zeros(iter_num, 1); %%%%%%%%%%%%%%%%%%%%%%% tic %% 初始化隶属度并归一 membership = zeros(height,width,cluster_num); for i=1:height for j=1:width member_sum=0; for k=1:cluster_num membership(i,j,k)=rand(); member_sum=member_sum + membership(i,j,k); end for p =1:cluster_num membership(i,j,p)=membership(i,j,p)/member_sum; end end end center = zeros(cluster_num,1); for o = 1:iter_num %迭代次数控制 %% 计算初始中心 for u = 1:cluster_num sum = 0; sum1 = 0; for h=1:height for t=1:width sum = sum + membership(h,t,u).^m * exp((-1) * (a(h,t) - center(u).^2) / (beta.^2)) * a(h,t); sum1 = sum1 + membership(h,t,u).^m * exp((-1) * ((a(h,t) - center(u))^2) / (beta.^2)); end end center(u) = sum / sum1; end for h = 1:height for t = 1:width for k = 1:cluster_num costfunction(o) = costfunction(o) + 2 * membership(h,t,k).^m * (1 - exp( -1 * ((a(h,t) - center(k)).^2)/(beta.^2))); temp =(1 - exp( -1 * ((a(h,t) - center(k)).^2)/(beta.^2))).^(-1 / (m -1)); top = 0; for p = 1:cluster_num top = top + (1 - exp((-1 * (a(h,t) - center(p)).^2) /(beta.^2))).^(-1 / (m -1)); end membership(h,t,k) = temp / top; end end end if display, fprintf(‘iter.count = %d, obj. fcn = %f\n‘,o, costfunction(o)); end if o >1 if abs(costfunction(o)-costfunction(o-1)) < threshold , break;end; end end toc %% 输出图像 newing = zeros(row,column); for i=1:row for j=1:column maxmembership=membership(i,j,1); index=1; for k=2:cluster_num if(membership(i,j,k)>maxmembership) maxmembership=membership(i,j,k); index=k; end end newimg(i,j) = round(255 * (1-(index-1)/(cluster_num-1))); end end subplot(2,2,1),imshow(uint8(a)); title(‘原图‘) subplot(2,2,2);imshow(I);title(‘加噪图像‘); subplot(2,2,3);imshow(uint8(newimg));title(‘KFCM分割后的图像‘);
可以得到结果:
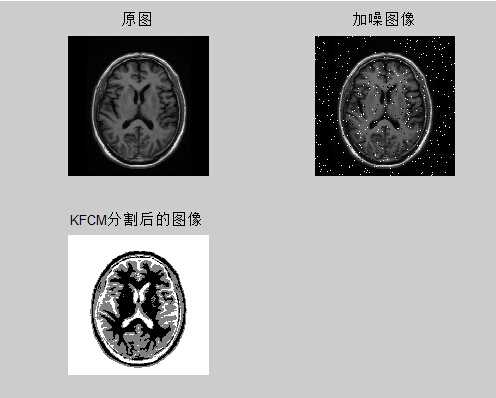
与之前的FCM的分割结果相比还是有很大的提升的。结合之前所分析的,考虑到空间数据之间的相关性,结合各点的邻域信息,在原代码中添加邻域信息:
%% 邻域信息 Xk = zeros(height,width); for i = 1:height for j = 1:width up = i - 1; down = i + 1; left = j - 1; right = j + 1; if (up < 1) up = i; end if (down > height) down = height; end if (left < 1) left = width; end if (right > width) right = height; end A = zeros(1,6); for x = up : down for y = left : right A = a(x,y); end end Xk(i,j) = mean(A); end end
这样可对算法进一步优化。
好了,将核方法应用到FCM算法今天就说这么多了,总而言之,核方法的应用确实使算法的性能提高了不少。
标签:
原文地址:http://www.cnblogs.com/ybjourney/p/4743893.html